by 
Sometimes, lay persons may think mathematics is a totally theoretical discipline you learn at school and the memory of which fades over time. But actually, mathematics is something that pervades the world far more than we imagine, also thanks to its practical applications, which are countless.
Today, one of the most popular areas of mathematics today is that of theoretical models to be applied to the most diverse physical phenomena for engineering applications.
We interviewed Edoardo Bocchi, a researcher at the Department of Mathematics, who told us about the THANAFSI (Theoretical analysis of fluid-structure interaction problems and applications) project he is working on.
Civil and coastal engineering require through and full understanding of the interaction between fluids and structures. To achieve this, two problems, among many others, are considered: the stability of suspension bridges under the action of the wind and the impact of ocean waves on marine energy converters.
Edoardo Bocchi was able to settle in Italy thanks to an MSCA Marie Skłodowska Curie Postdoctoral Fellowship from the European Union. In 2023 , 13 MSCA beneficiary researchers chose Politecnico di Milano as the location for their research project. The European grant is awarded to individual researchers for particularly promising projects in pioneering scientific fields or emerging technologies with high innovation potential and of public interest, with the aim of developing new expertise through international, interdisciplinary and intersectoral mobility.
For Edoardo Bocchi, this fellowship meant settling in Italy after a long experience abroad and a short period as a temporary research fellow at Politecnico di Milano. Winning the fellowship was a great satisfaction, as this has been the first major research project he submitted. And so, since last September, he started his project at Politecnico di Milano, where we met him in his office in the familiar ‘Nave’ building.
Hello, Edoardo. Could you please tell us about your academic journey to date…
My university career began at Università Statale di Milano, where I had both a Bachelor and a Master of Science programme in Mathematics, to finally graduate in 2016. I spent the last year on an Erasmus project at the University of Bordeaux, where I wrote my thesis. Subsequently, I went back to Bordeaux, where in 2019 I obtained my PhD in Applied Mathematics. After that, I was a postdoctoral researcher at the University of Seville for two and a half years. After the Covid-19 pandemics I had the idea of coming back to Italy.
And here I am, just 31 years old, at Politecnico di Milano. The fellowship I have won will allow me to continue my research for another two years at the Department of Mathematics.
Why this desire of yours of coming back to Italy?
Well, first of all, the distance: we were in the pandemic, and I wanted to get closer to my family. And then, I liked the idea of trying to make it in the country where I studied. My goal was to come back to Italy: the choice of Milan came later.
And why at Politecnico?
Politecnico is one of the few Italian universities that also has made a name abroad. But above all, the required topic for the research position was very close to what I had been working on for some time.
What difference do you find in doing research in Italy, compared to your long experience abroad?
I must admit that, on average, the job of a postdoctoral researcher abroad is paid better. Scholarships last longer, while in Italy they often last one year only and are then renewed.
It is also true that the Marie Curie fellowship offers a good funding. I have some funds of my own, so the fellowship allows me to be independent, attend conferences and also make myself known to external collaborators. It is precisely aimed to enhance the experience that a research period abroad can give you.
Let’s talk about your research. How would you describe it in a few words?
The focus of my research is a theoretical analysis of fluid-structure interaction problems.
The idea is to use mathematical analysis to improve the understanding of problems arising in maritime and coastal civil engineering, in the interaction between suspension bridges and the wind, which can generate deck oscillations, to prevent collapse and design reliable structures, as well as in the interaction between waves and marine energy converters to improve their efficiency.
My approach is therefore theoretical, I focus on the qualitative and theoretical study of mathematical models. This is different from a numerical, quantitative approach, which aims at the next stage, that of experimentation.
What civil engineering problems are you referring to?
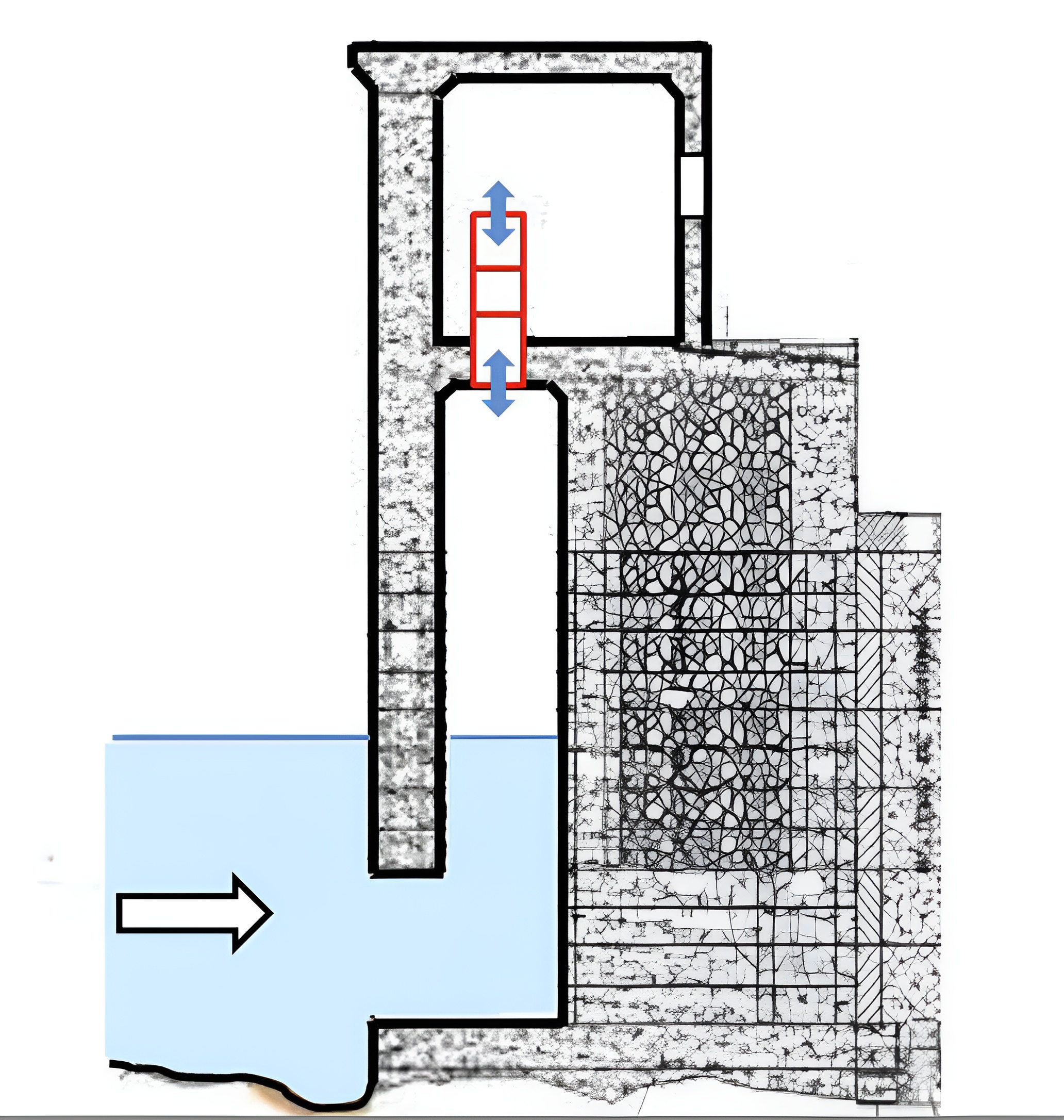
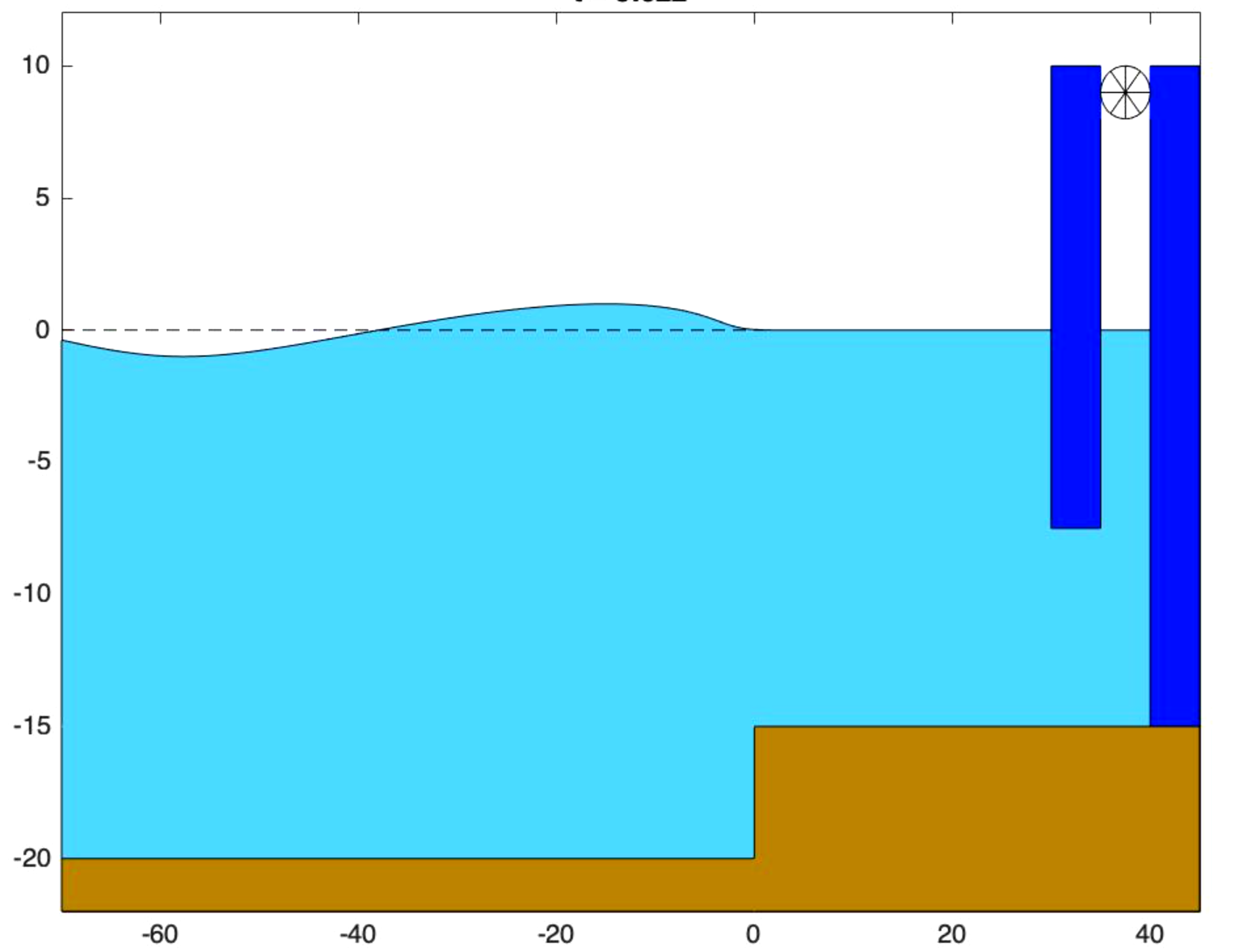
There are mainly two problems. The first is the stability of suspension bridges under the action of the wind. The second is the impact of ocean waves on certain types of marine energy converters known as Oscillating Water Columns (OWCs).
Let’s start with the second. In this case, waves arriving from offshore meet a partially open chamber on the coast. The incoming wave breaks against the outer structure of the chamber, causing part of the wave to pass through the opening and enter the chamber, going up and down (hence ‘oscillating’). Therefore, air changes in volume and is forced out through a slot at the top, through a turbine. As the turbine moves, it transforms free, clean energy into electrical energy. Energy that can be utilised by converting it.
Are there other examples you are working on?
Yes, the floating buoys in nearshore areas, i.e., in an area that is at an intermediate distance from the coast. The buoys are connected to the seabed by cables and linked to the coast by other cables. The very fact that the buoy floats creates mechanical energy, which in turn creates electrical energy.
Your models start from these phenomena
Yes, my job is precisely to derive mathematical models from the physical phenomenon. It is finding solutions that solve the problem. In the case I mentioned, the complexity is the interaction between structure and fluid.
And in the problem of the bridge structure, what is the model?
In this model, the structure is represented by the bridge, the fluid by the wind. Here you have to study the amount and type of forces that come into play with the bridge, e.g., the lift, magnitude and shape of the wind. Navier-Stokes equations are used to describe the flow of these fluids. Finding the solution is part of the qualitative study.
At the application level, the ideal condition would be a minimum lift, so that the bridge does not move, or moves as little as possible. To clarify what lift is, it is what makes an aircraft fly. It is a force perpendicular to the aircraft and it takes a large amount of lift to make the aircraft rise, which is different from the case of a bridge.
Are there any famous examples of structural stability studies?
A famous example of structural stability study is the Tacoma Narrows Bridge, which collapsed in 1940 within months of its opening. We have an extraordinary audiovisual document of its collapse, filmed with a camera. It can be seen that before the bridge collapsed, there were vertical wave motions caused by the interaction with the wind; afterwards, torsional motions can be seen, when the span starts to move and oscillate: it is these that created the collapse.
In our project we study, for example, what shape the span of a bridge should have in order to minimise the lift.
Another goal is to increase energy efficiency, correct?
In the ocean chamber we study the qualitative part. The next step is to approach the numerical part. We have to show that the solutions of simplified reality models are consistent with that which happens in experiments. If consistent, we can try to improve the efficiency of the energy converter.
Efficiency is the ratio of captured energy to incoming energy. In the ideal case, we gain all the energy. In reality, if this ratio is 0.5, and it is already a lot. The problem with these converters is that they have a lot of dispersion, greater implementation costs and therefore reduced gain. The question we ask ourselves is whether we can improve this energy efficiency, continuously pushing ourselves a little farther.
Where does your research stand in the project?
I am still at the beginning, I have to understand what kind of model to develop: not the most difficult one but one that reflects the qualitative properties of the system as closely as possible.
One of my goals is to reduce the complexity of the model without losing too much information and to make it cheaper to implement, and then to study the solution.
To give you an example, a model used in shallow water could also be applied in a tsunami model, retaining the value of the model because the ratio of sea depth to wavelength is small in both cases.
How do you go about your daily work?
I am part of the ‘theoretical fluid’ group in the Department of Mathematics, with whom I discuss mathematics, but I mainly work with my supervisor, Professor Filippo Gazzola, and collaborators in foreign universities (France, Spain).
Don’t expect big labs and white coats. I am a mathematician, so much of my work takes place in the office. My tools are a computer, pen and paper and a blackboard.
However, beyond the theoretical part, the project also includes other activities. There is the training part, which also includes a two-month period abroad to work with other colleagues. There is the popularisation part, during which we will go to upper secondary schools to talk about our research.
The popularisation part is very interesting, especially in mathematics. It cannot always be easy to attract students to such seemingly theoretical fields of research…
The disclosure part is very intriguing for a theoretical researcher like me. Many times, upper secondary school students do not realise that there is a lot of mathematics behind large projects such as bridges. It is nice to stimulate the interest of girls and boys in these topics, and thus attract them to choose a study programme in mathematics.
How did it all start with your love of mathematics?
Already in middle school, and then in upper secondary schools, I had a particularly easy time studying mathematics. It didn’t weigh me down, and in fact I liked it.
When I finished upper secondary school, the dilemma was: mathematics or engineering? I chose with my heart, I chose mathematics. At university I saw a whole other level, compared to what I was used to until then: it was not that easy.
During my Master of Science programme, I still had no idea that I would go on. It was then at a conference that I heard a professor talking about a model that described sea waves, without structures. Before long, I was surprised at my interest in the rigorous and mathematical description of phenomena such as sea waves. It was the first time I had seen a concrete (albeit theoretical) application of concepts that until then I had only studied.
And how did you end up abroad?
Thanks to this new interest of mine, I decided I wanted to do my Master of Science thesis in Bordeaux, where Professor David Lannes, one of the leading experts in wave modelling, works. After his positive response and subsequent proposal to continue with a PhD, I entered the world of mathematical modelling of fluid mechanics. I discovered a large international community of mathematical researchers who study these models from a rigorous point of view.
Where do you see yourself in a few years?
The first thought is that I would like to stay here. The kind of research I do here is mathematics with an eye to application, where application is the physics of models, and it is this research that I like.
The challenge is to find a permanent position for me here at Politecnico, after the MSCA fellowship. It is a strong experience in my CV, and I hope it will help me in my future academic career.
What is the aspect you did not expect to find in the work you are doing?
I have only recently come into contact with the popularisation part of the project, and I must admit that it is very stimulating. Writing the project for the fellowship helped me to approach the world of outreach and communication. Openness to the outside world is also the direction in which the European Open Science guidelines are pushing.
Trying to explain complex concepts in a simple way to the world outside the laboratory is a real challenge for a theoretical mathematician. Research is a truly fascinating tale.